In order for a computer to understand words we first need to turn it into numbers, since computers relate to everything through numbers stored as binary. We already store individual letters, numbers and symbols as binary using the ASCII table.
| Character | ASCII Code (Decimal) | Binary Representation |
|---|---|---|
| A | 65 | 01000001 |
| a | 97 | 01100001 |
| B | 66 | 01000010 |
| b | 98 | 01100010 |
| 0 | 48 | 00110000 |
| 1 | 49 | 00110001 |
| @ | 64 | 01000000 |
| # | 35 | 00100011 |
We could do something like this for words, giving each an explicit number, but words are a bit more complex than letters. Words, for example, have meanings which change given the content, such as butter the roll or butter you up.
What we want is a way to represent words which can help the computer relate the words of a sentence or document with each other in order to better understand the context. One way to do this is using vectors.
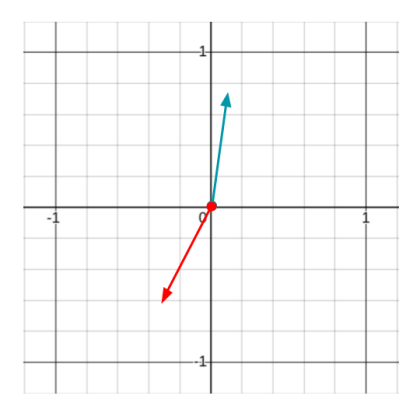
The above are two-dimensional vectors, but the vectors which are used when representing words in language models could be thousands or even millions of dimensions.
Different words will point in different directions, and with the algorithms used to create these vectors, some interesting properties can form. For example, vectors pointing in the same direction might represent similar words, while those pointing in opposite directions could be opposites.
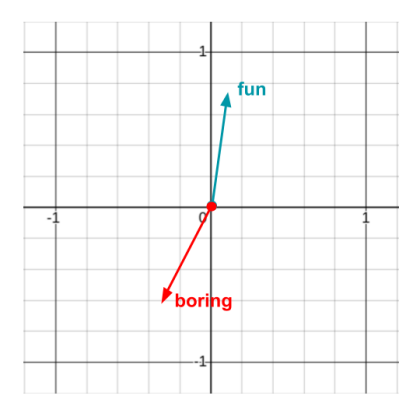
The magnitude (length) of the vector can also have meaning, but it’s more common for algorithms to place greater importance on the direction. Many of the algorithms disregard the magnitude entirely.
Aside from looking at the proximity of words, another interested property can emerge using basic vector arithmetic. For example we could do something like:
vector("coffee") + vector("milk") => ?If you remember from vector addition, this will have the effect of something like this:
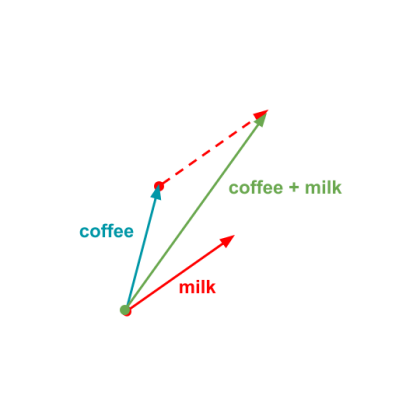
But if we normalize (scale it down to be a vector or length 1) the vector then we’ll get something like:
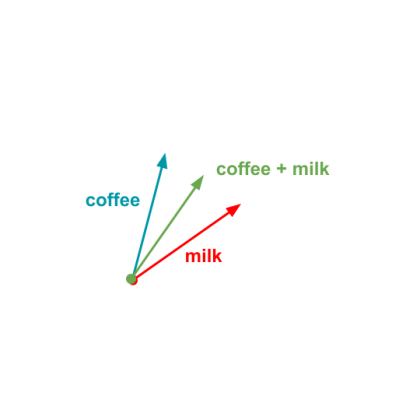
Where this vector ends we might find words such as latte, cappucino, macchiato and such. The interesting thing is that you can perform more sophisticated operations to find similiar relationships with other words.
vector("Paris") - vector("France") + vector("Tokyo") => ?This would likely get you close to Japan, provided the text you’ve based your word vectors on includes information about these locations. That’s part of the reason a large corpus (body of text) covering a range of topics is best.
While the above provides intuition on what we can do with vectors, it doesn’t provide any indication on how they are created. There are many algorithms which can be used to construct them, often referred to as embeddings:
To summarize, we use vectors to represent words because they’re mathematically convenient and they allow us to discover relationships between words.