You’ll hear a lot about embeddings when you start looking at machine learning models. What an embedding is, in broad terms, is a way to take your data, whatever it may be, and turn it into something which can be used by machine learning models. These days, most models are based on neural networks, and require some sort of fixed-length input represented as numbers. I mean, all things on your computer are already represented as numbers, but embeddings give us more meaningful numbers.
Embeddings are a way not only to give us this fixed-length representation, but they also help to show relationships between the objects in our data. While vectors are certainly the most used method today to find these relationships, there are also graph-based models, symbolic representations and even quantum embeddings.
The basic idea is that we can take a data set, whether it’s a set of texts, images, or even videos or sounds and build a mathematical understanding of what makes them the same and different from one another by running it all through some algorithm.
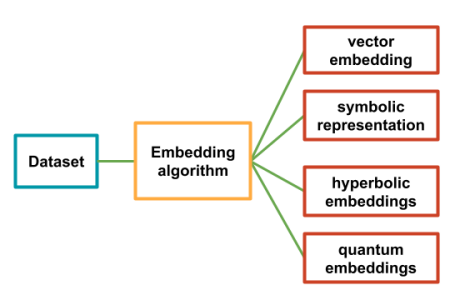
By mathematical understanding, I mean something like a co-occurrence matrix, which counts how often words appear next to each other, or a vector model which creates a vector every word (more likely a token), with vectors that are near each other having similar meaning.
With words, there are many different methods for doing this, each of which is has their own method for establishing these relationships:
With images we might use a deep neural network and train it on a set of images, later using the internal structure (a layer, for example) of the network as a representation of the overall set of images.
I will leave the technical how of each method for their own individual posts, but here just know that the goal is to take data and do the following:
We should have points (1) and (2) covered, but we haven’t talked about (3) yet.
Dimensionality is another word you’ll hear come up again and again. To give you an example you can look at one-hot encoding, or read on.
Let’s say I have a set of texts that I want to run through an LLM or some other model. I want to train this model to give me answers based on this set of texts. Let’s also say for the sake of simplicity that in all these books there are only five words: “a”, “and”, “dog”, “cat”, “the”.
A dog and cat. The dog. A cat. A dog. A dog and the cat. The cat and the dog.
In order to train my model I need to transform the text into a form that it can use. As mentioned, most machine learning models use a fixed-length input. I could make the input as long as my longest word and feed things in character, padding out the rest of the word with some filler (represented by % below).
representation = [“dog”, “cat”, “the”, “and”, “a%% “]But this doesn’t give us any idea of how these words relate to one another in the text. Assuming the texts are mostly grammatically correct, it’s unlikely for us to see combinations of words like “the a” or “cat the.” When training our model we’d like to give answers which fit the style of the input as being grammatically correct.
To do this, we’ll use one of the methods shown above, Word2Vec for example, to create an embedding. This embedding will assign a vector to each word, and words which are more closely related will be pointing in the same direction. One-hot encoding gives each vector its own axis:
dog = [1, 0, 0, 0, 0]
cat = [0, 1, 0, 0, 0]
…The above vectors are drawn on a space with five dimensions, which I’d love to draw, but I was never the best artist in school.

But if I have five words in my books and five numbers in my vectors, then I haven’t really reduced the dimensionality, have I? That’s where the algorithms come in. As mentioned, the details of this I will leave for each individual page, but here you should note that it’s compressing the representation of the words into a lower dimensionality, thus saving space needed for each word.
dog = [1.2, 1.0]
cat = [1.1, 0.9]
…In this reduction there may be some information lost, but just think of the savings!
Once you’ve created the embeddings, what you have is essentially a lookup table for elements of your data set. If it’s textual data those could be words or parts of words, more often called tokens, and when training the model will look up the words in your embedding and send them on to be used in training or later in inference.