If all you want is the code, then head over to the repo. There is also a video.
This is the start of a project I’ve wanted to do for a while now, building a websocket-based game from the ground up using Rust. I’d like to do it while also teaching some of the fundamentals of the language.
By ground up I mean using only the standard library for anything which does not touch the browser, and with the browser only as much as needed. That means eventually using web assembly. By teaching the fundamentals I mean I’m going to take it slow and explain key concepts, possibly multiple times across the different articles. I will assume that the reader knows how to install Rust, use the basics of cargo and have some programming background in other another language.
Each of these articles will act as a sort of project unto themselves. I’ll cover, and recover concepts as I go, both for your benefit and mine. In truth, most of my stuff is for my own use. By writing things down and explaining them I’m better able to understand the concepts and remember them.
With all that out of the way we can start building, but before we get into any code, we’ll take a look at the websocket protocol and the parts of it we’re going to implement in the next few articles. If you’re already familiar with it, you can skip to the next section.
The websocket protocol is lengthy, and I don’t want to get too bogged down in its details, but it’s important to have a general overview of how things work. Below is a diagram which gives a high-level of how a connection is made and later closed:
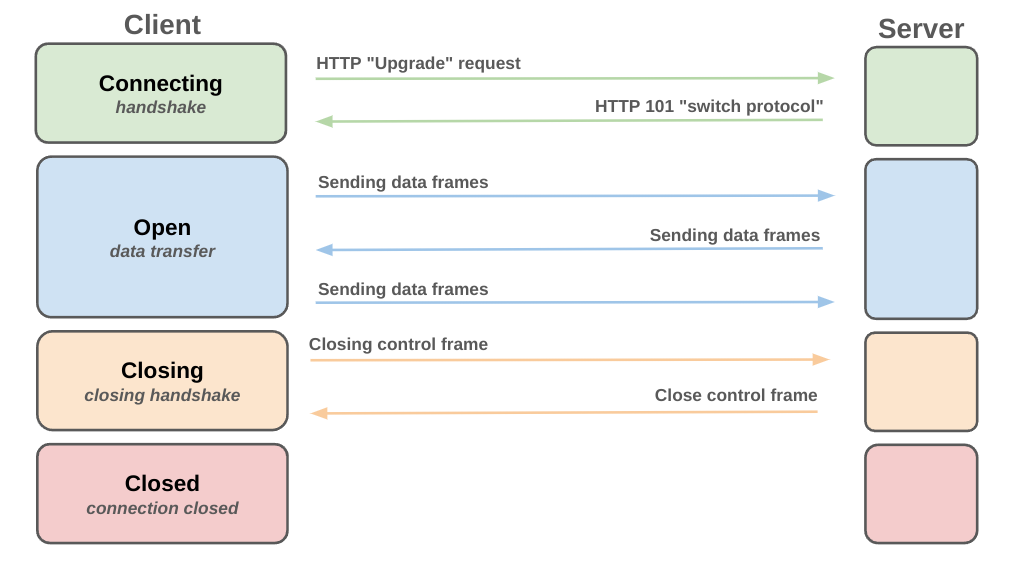
As you can see there are four states we can be in: connecting, open, closing, and closed. In this article, we’re only going to worry about the connecting state and even then, only part of that initial handshake.
The opening handshake is intended to be compatible with HTTP-based server-side software and intermediaries, so that a single port can be used by both HTTP clients talking to that server and WebSocket clients talking to that server.
What this says is that your website and websocket connection can coexist on the same port, which is generally 80. From the perspective of the client this is like calling a typical HTTP route to request a webpage, such as https://www.somesite.com/start-game, but instead of using https we switch to wss or ws, depending on if it’s secure or not secure, respectively.
This initiates the handshake, with the client making an HTTP request that looks something like:
get /connect http/1.1
host: www.example.com
upgrade: websocket
connection: upgrade
sec-websocket-key: dghlihnhbxbszsbub25jzq==
origin: http://example.com
sec-websocket-protocol: chat, superchat
sec-websocket-version: 13This is in comparison to the typical HTTP GET request which might look like this:
GET /index.html HTTP/1.1
Host: www.example.com
User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/webp,*/*;q=0.8
Accept-Language: en-US,en;q=0.5
Accept-Encoding: gzip, deflate, br
Connection: keep-aliveAs you can you tell there are a number of differences, but the one we’re going to be most concerned with in this article is the Sec-WebSocket-Key. This is a SHA-1 hash that has been base64 encoded. I’m going to skip the other sections for now, but in the next article we’ll come back to the protocol section and discuss what is meant by chat and superchat.
If you’re at all familiar with SHA-1, you’ll know that it is vulnerable in cryptographic scenarios where collision resistance is important. Collision resistance is the ability of a hash algorithm to NOT produce the same output given two different inputs, but in truth we don’t really care about that with websockets. We’re only using the SHA-1 algorithm for protocol confirmation and validation. In essence, it’s just there to make sure we want to upgrade to websockets, not to secure information.
With that out of the way, let’s look at the response from the server after the above request has been sent:
HTTP/1.1 101 Switching Protocols
Upgrade: websocket
Connection: Upgrade
Sec-WebSocket-Accept: s3pPLMBiTxaQ9kYGzzhZRbK+xOo=You’ll notice we have the pair Sec-WebSocket-Key in the request and Sec-WebSocket-Accept in the response. The Key is a 16 byte base64 encoded string, while the Accept is a bit more complex.
To create the response, the server takes the key and performs the following steps:
The only confusing part here, I hope, is with regard to the GUID and how it was chosen. Here the official protocol docs say:
and concatenate this with the Globally Unique Identifier “258EAFA5-E914-47DA- 95CA-C5AB0DC85B11” in string form, which is unlikely to be used by network endpoints that do not understand the WebSocket Protocol.
Unfortunately, there seems to be no particular reason why this exact GUID was chosen. Maybe there’s an inside joke we’re not privy to, or maybe the creators of the websocket protocol have no sense of humor.
All this brings us to the first step in creating our websocket server, and that’s getting the handshake done, but to do that we’ll need to implement SHA-1 and base64 encoding, which is exactly what we’ll do, starting in this article with SHA-1.
As noted above, SHA-1 is a vulnerable hash function which shouldn’t be used to secure information, but is used here as means to validate a request to upgrade an existing HTTP connection to websockets. In implementing it we can gain some insight into future iterations of SHA and other hashing functions, though from what I’ve read SHA-3 varies significantly from the first two. At the very least you’ll come away with an understanding of what a hashing algorithm does in principle. Of course I’ve said all this with the assumption that you know what hashing algorithm is, and if that’s not the case then please read on. If you already have a decent understanding of hashes feel free to move on and start building.
This is a fairly large topic, and I don’t want to get into too many details, so let’s take the simple definition that a hash algorithm is used to take input of any size and return a fixed-length string. Information goes in and a string of equal length comes out, no matter how large the input is.
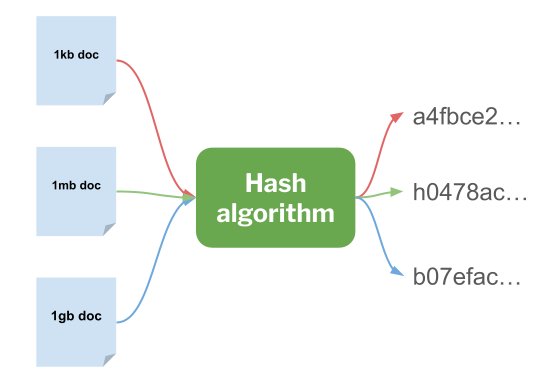
There are a few special properties we need to keep in mind:
1 The probability of two inputs having the same output should be infinitesimally small. Like finding a needle in a universe-sized haystack, but even more unlikely.
You may also hear hash algorithms be referred to as a type of one-way function, which have a number of uses in cryptography. We don’t want to get too far down this rabbit hole, and instead focus on getting past the first step of implementing websockets. For now, keep in mind the three points above as we dive into implementing SHA-1.
Create an initial Rust project using cargo and then another file alongside main.rs called sha1.rs. In our sha1.rs file we’re going to create a struct called Sha1 and outline a function to create an instance of it.
// sha1.rs
pub struct Sha1;
impl Sha1 {
pub fn new() -> Self {
Sha1 {}
}
}If you’re not familiar with structs, they are a way to define a data type, much like using a class in an object-oriented language. I will note that they are not classes, though, as they lack many of the features which define a class, like inheritance.
If you are familiar with a language that uses structs this setup might look a little weird, either because you’re not used to a function being directly associated with a struct (like in C, unless done with pointers) or because the functions are separate from the struct itself (C++ or C#, for example).
One thing that may look familiar if you’ve done any Python or Ruby programming is the Self. In other languages this is similar to using this in Java, JavaScript, C# and other languages. In Rust there are two selves, the uppercase Self and the lowercase self:
Let’s test this out and create a few instances of Sha1 to see how things work. Back in main.rs we’ll import our module and create an instance of Sha1:
// main.rs
mod sha1;
use sha1::Sha1;
fn main() {
let mut sha1 = Sha1::new();
}Now we have a data type Sha1 which uses a separate block of code defined by the keyword impl, read as implementation, which contains associated functions. We use those functions through a double colon, like with ::new().
You can actually create as many implmentation blocks as you want for any given struct. For example, if I want to make a another function called foo for Sha1 I could do this:
// sha1.rs
pub struct Sha1;
impl Sha1 {
pub fn new() -> Self {
Sha1 {}
}
}
impl Sha1 {
pub fn foo() {
}
}This can be confusing to people new to Rust, and can seem messy at times, but there are good reasons for it that mostly have to do with traits. Getting into traits is probably too much at this point, but we’ll make sure to come back to it in a later article. For now, just know the following:
Now that we’ve got some of the basics out of the way, let’s start hashing.
Remember that our goal is to be able to take in some key, a string, and produce a hash value. To do that our Sha1 type will need a hash function, which at first we’ll create as such:
// sha1.rs
pub struct Sha1;
impl Sha1 {
pub fn new() -> Self {
Sha1 {}
}
pub fn hash(&mut self, key: &str) -> [u8; 20] {
}
}And we’ll call it in our main.rs like this:
mod sha1;
use sha1::Sha1;
fn main() {
let mut sha1 = Sha1::new();
let hash = sha1.hash("TESTING");
}Next, let’s look at the steps to properly construct our hash. We’ll break this process it into two parts. In the first we’ll pad our message and in the second construct the message schedule. In this case, message refers to our input, and the message schedule refers to the scrambled hash that comes out of the algorithm. Below are the steps for padding our message:
To do this we’ll create a separate function in the Sha1 impl block called pad_message which takes a string as a parameter and returns a Vec, which is to say a vector of unsigned integers of 8-bits or 1-byte in length.
impl Sha1 {
pub fn new() -> Self {
Sha1 {}
}
pub fn hash(&mut self, key: &str) -> [u8; 20] {
}
fn pad_message(&self, input: &str) -> Vec<u8> {
}
}You’ll notice in the above I use the word array, while here we’re using vectors. I wanted the steps to be more general, and not give the impression one needed a vector. We could, in fact use arrays, but since arrays are static in length, using Rust’s vectors makes more sense, as they allow us a flexible data structure to do the push operations in steps 3-5. If you’re not familiar with vectors, they are similar to a list in Python, and allow us to more easily push, pop and slice up data.
This is easy enough and done by:
fn pad_message(&self, input: &str) -> Vec<u8> {
let mut bytes = input.as_bytes().to_vec();
}You’ll notice how Rust allows for chaining of functions, first converting to bytes, then to a vector, which is a style common in functional programming. There’s actually quite a bit Rust borrows from functional programming, as we’ll see going forward.
On an interesting sidenote, this idea of chaining (composable functions) dates all the way back to the original days of Unix and work by Ken Thompson, Brian Kernighan and others. There’s a nice Corecrusive episode with Kernighan about the origin of the pipe operator and writing composable programs.
Next, we’ll stash the lenght of the original input for use in step (5).
// sha1.rs
fn pad_message(&self, input: &str) -> Vec<u8> {
let mut bytes = input.as_bytes().to_vec();
// Save the original message length for appending below.
let original_bit_length = bytes.len() as u64 * 8;
}The reason we’re multiplying by 8 here is not just because its a lucky number in Chinese culture, but because we’re appending the bit-length as opposed to the character length of our input data. The reason for any sort of appending has to do with ensuring that the output hash varies based on input.
For example, with two similar messages like ABC and ABCD the algorithm might produce values which end up colliding, meaning they produce the same hash. While they won’t immediately do so, it’s possible that values which are somewhat close can end up producing the same values after initial calculations due to using wrapping bitwise addition or logical operations. The addition of the length provides additional input dependent randomness which keeps the odds of this happening extremely small.
This is added at the end of our data to delineate the start of the padding.
// sha1.rs
fn pad_message(&self, input: &str) -> Vec<u8> {
let mut bytes = input.as_bytes().to_vec();
// Save the original message length for appending below.
let original_bit_length = bytes.len() as u64 * 8;
// Append the '1' at the most most significant bit: 10000000
bytes.push(0x80);
}We then pad it out with zeros such that we leave 64-bits of the last 512-bits for step (5).
// sha1.rs
fn pad_message(&self, input: &str) -> Vec<u8> {
let mut bytes = input.as_bytes().to_vec();
// Save the original message length for appending below.
let original_bit_length = bytes.len() as u64 * 8;
// Append the '1' at the most most significant bit: 10000000
bytes.push(0x80);
// Pad with '0' bytes until the message's length in bits modules 512 is 448.
while (bytes.len() * 8) % 512 != 448 {
bytes.push(0);
}
}This means we have some N number of 512-bit or 64-byte chunks where the last chunk is missing 64-bits or 8-bytes.
We then take the unsigned 64-bit integer that is the length of the original input, and complete the array we constructed in step (4).
// sha1.rs
fn pad_message(&self, input: &str) -> Vec<u8> {
let mut bytes = input.as_bytes().to_vec();
// Save the original message length for appending below.
let original_bit_length = bytes.len() as u64 * 8;
// Append the '1' at the most most significant bit: 10000000
bytes.push(0x80);
// Pad with '0' bytes until the message's length in bits modules 512 is 448.
while (bytes.len() * 8) % 512 != 448 {
bytes.push(0);
}
// Append the original message length.
bytes.extend_from_slice(&original_bit_length.to_be_bytes());
bytes
}You’ll notice the seemingly errant bytes at the end. In Rust the last variable or statement which returns a value is automatically returned as long as we haven’t place a semincolon at the end. You can all put a return if you’d like, but it’s more common to see functions without it.
Now let’s test it’s working with a few calls and print lines.
// sha1.rs
impl Sha1 {
pub fn new() -> Self {
Sha1 {}
}
pub fn hash(&mut self, key: &str) -> [u8; 20] {
let msg = self.pad_message(key.as_ref());
println!("{:?}", msg);
}
fn pad_message(&self, input: &str) -> Vec<u8> {
...
}
}You should have a called to hash in main.rs, as written earlier, so when running the program you will see an array of integers, with mostly zeros, printed out. One odd thing about this print statement, though, is the {:?}. Normally, we can use {} as placeholder for the value we want to print, but here we’ve added the colon question combination as a way to noting we want debug formatting. This is done when whatever we’re printing does not have implement Display and provide its own default output method, which vector does not.
And with that we’ve completed padding of our message and are ready to move onto the main part of SHA-1. You might be wondering the reasoning between a lot of this, for example why 512-bits? For many of these things it’s hard to pin down a reason why, but there are likely some historical reasons. In this case 512 was used by US government in their algorithms. Other algorithms like SHA-3 use 1024 bits, but all algorithms will use powers of 2 since computers function in binary. I suppose if we were using a ternary computer we’d use a power of 3.
We’re now ready to jump into the depths and implement the actual algorithm, starting with defining a few constants. At the top of your sha1.rs file place these:
// sha1.rs
// These constants are derived from the fractional parts of the square roots of the first five primes.
const H0: u32 = 0x67452301;
const H1: u32 = 0xEFCDAB89;
const H2: u32 = 0x98BADCFE;
const H3: u32 = 0x10325476;
const H4: u32 = 0xC3D2E1F0;These numbers are the first step of every SHA-1 hashing algorithm, and are derived from the fractional parts of the square root of the first five primes: 2, 3, 5, 7 and 11. These values are sufficiently random to provide a good jumping off point towards creating outputs which vary significantly from one another.
Now, let’s look at the steps we’re going to take in order to do the actual hashing:
That’s a lot of steps, but we’ll go slowly through each of these and explain the reasoning as best I can. Some will end up being quite short, while a few, like (7) will take up the bulk.
These variables will hold the running result of all our hashing, and be what we concat together at the end of it all to produce what is known as a hash digest or hash.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
}
}Rust does a pretty good job of type inference, but you can equally state those explicitly.
For this part we’ll use the chunks function which is implemented on anything that can be iterated over, like our vector, and returns a chunk equal to the value of its type, which in our case is a u8 or byte.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
}
}
}This means we’ll get 64 chunks that are each a byte, for a total of 512 bits.
I’m using the term one-time here to indicate that they will be used for one iteration of the outside loop, then reset the following loop.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
}
}
}For steps (4) to (6) I’ve broken the logic off into a separate function, which is added to the Sha1 impl block, called build_preliminary_schedule, not because it’s necessary for it to be a separate function, but for learning purposes I think it can help to break things into sections.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
let schedule = self.build_preliminary_schedule(chunk);
}
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
let mut schedule = [0u32; 80];
}
}This takes in our 64-byte chunk and returns an 80-byte chunk. We’ve done the first step of defining this 80-byte chunk above.
Here we use our schedule array and fill in the first 16 unsigned 32-bit integers of the 80 it can hold.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
let mut schedule = [0u32; 80];
// Initialize the first 16 words in the array from the chunk.
for (i, block) in chunk.chunks(4).enumerate() {
schedule[i] = u32::from_be_bytes(block.try_into().unwrap());
}
}
}At this point the data is still recognizable, just converted into a different form.
The rest of the array is filled by using the original values while performing an XOR operation over the previous values.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
let mut schedule = [0u32; 80];
// Initialize the first 16 words in the array from the chunk.
for (i, block) in chunk.chunks(4).enumerate() {
schedule[i] = u32::from_be_bytes(block.try_into().unwrap());
}
// Extend the schedule array using previously defined values and XOR (^) operations.
for i in 16..80 {
schedule[i] = schedule[i - 3] ^ schedule[i - 8] ^ schedule[i - 14] ^ schedule[i - 16];
schedule[i] = schedule[i].rotate_left(1);
}
schedule
}
}Like most languages, Rust allows for a number of different logical operators. In SHA-1 we only need to worry about XOR (^), AND (&), OR(|) and NOT(!). You’ll notice that we also do a rotation left which means we’re shifting the entire array one to the left and wrapping the result that falls off to the other side.
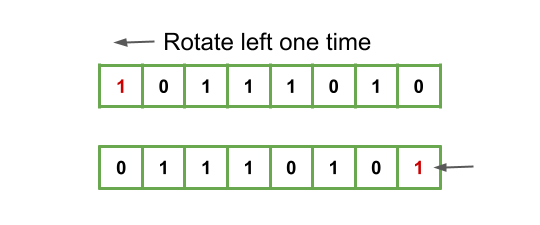
These operations will perform an initial shuffling of the original input. After we done that we return schedule at the end.
Here we start a loop which will end at step (9).
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
// Get the message schedule and copies of our initial SHA-1 values.
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
let schedule = self.build_preliminary_schedule(chunk);
// Main loop of the SHA-1 algorithm using predefind values based on primes numbers.
for i in 0..80 {
let (f, k) = match i {
0..=19 => ((b & c) | ((!b) & d), 0x5A827999),
20..=39 => (b ^ c ^ d, 0x6ED9EBA1),
40..=59 => ((b & c) | (b & d) | (c & d), 0x8F1BBCDC),
_ => (b ^ c ^ d, 0xCA62C1D6),
};
}
}
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
}
}This is really the heart of the SHA-1 algorithm. It uses a series of logical operations to produce the value f of the tuple (f, k). In each of these cases the k is a constant given in hexadecimal form. These constants are 230 times the square roots of 2, 3, 5 and 10, from the first to the fourth calculation, respectively. According to the Wikipedia entry the use of these constants caused some problems:
However they were incorrectly rounded to the nearest integer instead of being rounded to the nearest odd integer, with equilibrated proportions of zero and one bits. As well, choosing the square root of 10 (which is not a prime) made it a common factor for the two other chosen square roots of primes 2 and 5, with possibly usable arithmetic properties across successive rounds, reducing the strength of the algorithm against finding collisions on some bits.
Before we discuss these logical operations I want to discuss some syntax you may not have seen before if you’re new to Rust, and that’s the use of match.
In Rust, pattern matching is something you will see everywhere. Here, we match on the index of the array i using four patterns denoting groups of 20 numbers up to and including 80. The syntax 0..=19 is matching on the range 0 to 19 including 19.
Here is an example of a simpler match statement assuming we have come command line menu asking us to make options about a file:
// Example
fn main() {
let day_type = 2;
// print CLI menu
let message = match operation {
1 => remove_file(),
2 => move_file(),
3 => rename_file(),
_ => null_action()
};
println!("{}", message);
}In this the user would be asked to press a key 1-3 and then some action would be performed on that file. You can match over anything you want, from integers to strings to ranges. You can even make on a range of strings like ‘a’..=’d'.
Within the SHA-1 match statement we also have a _ which is default, matching anything not picked up by the previous three patterns. Whenever one of these patterns matches it will return the value of the statement to the right of it, which in each case should be a tuple of two values. This is assigned to (f, k). Note, when using a match like this all tuples must return the value types or else it won’t compile.
With that out of the way, let’s get back to the four f operations performed on each set of 20 values from the schedule array. These operations are logical operations of the types: choose, parity, majority and parity.
Choose works by choosing c when b == 1 and d when b==0.
Majority outputs the majority of b, c and d.
Parity here means a bitwise operation as opposed to the additional bit used in network communications error checking algorithms. That operation is an XOR in the case of the indices 20-39 and 60-7.
Each of these has a role to play, with parity introducing non-linearity via the use of XOR which supposedly does something to help prevent attacks via linear cryptanalysis. All these methods provide some form of confusion or diffusion.
To put it simply, confusion means that we’re trying to make the relationship between the changes to our input and the corresponding output as disconnected as possible. One small change to the input should create a wholly different random output, and by twiddling the input slightly we shouldn’t gain any information from the output that might help us determine a connection between the two. Diffusion means that we want our input to affect as much of the output as possible.
After we’ve calculated the f and k values, but still in the loop, we are going to set it up so that these changes will ripple through all parts of our one-time values. The temp value is the first step towards doing that.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
// Get the message schedule and copies of our initial SHA-1 values.
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
let schedule = self.build_preliminary_schedule(chunk);
// Main loop of the SHA-1 algorithm using predefind values based on primes numbers.
for i in 0..80 {
let (f, k) = match i {
0..=19 => ((b & c) | ((!b) & d), 0x5A827999),
20..=39 => (b ^ c ^ d, 0x6ED9EBA1),
40..=59 => ((b & c) | (b & d) | (c & d), 0x8F1BBCDC),
_ => (b ^ c ^ d, 0xCA62C1D6),
};
let temp = a
.rotate_left(5)
.wrapping_add(f)
.wrapping_add(e)
.wrapping_add(k)
.wrapping_add(schedule[i]);
}
}
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
}
}I’m not entirely sure the rationale behind the order, nor why we add the schedule[i] at the end.
Now update our values:
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
// Get the message schedule and copies of our initial SHA-1 values.
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
let schedule = self.build_preliminary_schedule(chunk);
// Main loop of the SHA-1 algorithm using predefind values based on primes numbers.
for i in 0..80 {
let (f, k) = match i {
0..=19 => ((b & c) | ((!b) & d), 0x5A827999),
20..=39 => (b ^ c ^ d, 0x6ED9EBA1),
40..=59 => ((b & c) | (b & d) | (c & d), 0x8F1BBCDC),
_ => (b ^ c ^ d, 0xCA62C1D6),
};
let temp = a
.rotate_left(5)
.wrapping_add(f)
.wrapping_add(e)
.wrapping_add(k)
.wrapping_add(schedule[i]);
e = d;
d = c;
c = b.rotate_left(30);
b = a;
a = temp;
}
}
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
}
}Here we see that the changes we create ripple, or diffuse, through the values. The big changes happen in a and after the first time through a becomes b and b becomes c and so on. We then use e in creating our temp value. With each iteration we are both mixing, but also making it so that a change in any portion of the original input will diffuse through all values.
Repeat for all 80 values in the schedule array.
Lastly, after we’ve completed the the mixing for a single chunk we’ll accumulate the changes in our h0-h4 variables using a wrapping_add, which I explain below.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
// Get the message schedule and copies of our initial SHA-1 values.
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
let schedule = self.build_preliminary_schedule(chunk);
// Main loop of the SHA-1 algorithm using predefind values based on primes numbers.
for i in 0..80 {
let (f, k) = match i {
0..=19 => ((b & c) | ((!b) & d), 0x5A827999),
20..=39 => (b ^ c ^ d, 0x6ED9EBA1),
40..=59 => ((b & c) | (b & d) | (c & d), 0x8F1BBCDC),
_ => (b ^ c ^ d, 0xCA62C1D6),
};
let temp = a
.rotate_left(5)
.wrapping_add(f)
.wrapping_add(e)
.wrapping_add(k)
.wrapping_add(schedule[i]);
e = d;
d = c;
c = b.rotate_left(30);
b = a;
a = temp;
}
// Add the compressed chunk to the current hash value.
h0 = h0.wrapping_add(a);
h1 = h1.wrapping_add(b);
h2 = h2.wrapping_add(c);
h3 = h3.wrapping_add(d);
h4 = h4.wrapping_add(e);
}
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
}
}A wrapping add will prevent values from capping out after an addition, instead resetting them back to 0 and continuing with the addition. For example, if I have an unsigned 8-bit integer the largest value I can hold is 11111111 or 255. If I add 1 to that I have the choice of discarding the 1 or using a wrapping add. The wrapping add resets us back to 00000000. In our case, with all the additions we’re doing this a highly desirable, otherwise we’d likely end up with every value maxed out by the time we were done.
Finally, we do all these steps for every chunk in our original input data and then concat the result.
// sha1.rs
impl Sha1 {
pub fn hash(&mut self, key: &str) -> [u8; 20] {
// Initialize variables to the SHA-1's initial hash values.
let (mut h0, mut h1, mut h2, mut h3, mut h4) = (H0, H1, H2, H3, H4);
// Pad our key
let msg = self.pad_message(key.as_ref());
// Process each 512-bit chunk of the padded message.
for chunk in msg.chunks(64) {
// Get the message schedule and copies of our initial SHA-1 values.
let (mut a, mut b, mut c, mut d, mut e) = (H0, H1, H2, H3, H4);
let schedule = self.build_preliminary_schedule(chunk);
// Main loop of the SHA-1 algorithm using predefind values based on primes numbers.
for i in 0..80 {
let (f, k) = match i {
0..=19 => ((b & c) | ((!b) & d), 0x5A827999),
20..=39 => (b ^ c ^ d, 0x6ED9EBA1),
40..=59 => ((b & c) | (b & d) | (c & d), 0x8F1BBCDC),
_ => (b ^ c ^ d, 0xCA62C1D6),
};
let temp = a
.rotate_left(5)
.wrapping_add(f)
.wrapping_add(e)
.wrapping_add(k)
.wrapping_add(schedule[i]);
e = d;
d = c;
c = b.rotate_left(30);
b = a;
a = temp;
}
// Add the compressed chunk to the current hash value.
h0 = h0.wrapping_add(a);
h1 = h1.wrapping_add(b);
h2 = h2.wrapping_add(c);
h3 = h3.wrapping_add(d);
h4 = h4.wrapping_add(e);
}
// Produce the final hash value as a 20-byte array.
let mut hash = [0u8; 20];
hash[0..4].copy_from_slice(&h0.to_be_bytes());
hash[4..8].copy_from_slice(&h1.to_be_bytes());
hash[8..12].copy_from_slice(&h2.to_be_bytes());
hash[12..16].copy_from_slice(&h3.to_be_bytes());
hash[16..20].copy_from_slice(&h4.to_be_bytes());
hash
}
/// Builds the message schedule array from a 512-bit chunk.
fn build_preliminary_schedule(&mut self, chunk: &[u8]) -> [u32; 80] {
}
}This result will be 20 bytes in length or 160 bits, which gives us 2160 possible hashes.
The final code is here. If you want to test it against a known SHA-1 Rust library, you can do so in this Rust playground.
This was quite a long article, so my apologies. The next one on doing base64 conversion will be significantly shorter, though after that we’ll start on the websocket server which could also be tome length.
If you have any questions or corrections, feel free to send me an email: thespatula @ fastmail.com. (Sorry, I need to break that up to reduce spam from bots scraping)